Nim游戏的必胜策略和Xor运算的神奇应用
上一篇日志里介绍了Nim游戏,他的必胜策略可不是那么好想的。这个游戏貌似很久以前就已经有了,可是必胜策略直至20世纪初才被哈佛大学的一个叫做Charles Leonard Bouton的数学家找到,可见其思维难度;可是,这个必胜策略却只要由一个运算就搞定了:Xor(异或)运算,可见Xor运算之神奇。没有好好学过程序设计的人估计对Xor运算不甚熟悉,更不可能知道他的神奇应用了,因此我先说一说Xor运算。
Xor运算是位运算的一种,和And、Or运算类似,假如a、b都是布尔变量,则a Xor b被定义为:a、b相异则为真(所以中文名字叫做异或),a、b相同则为假。其真值表为:1Xor0=1, 0Xor1=1, 1Xor1=0, 0Xor0=0。众所周知,位运算也可以用于两个数之间,其定义就是把这两个数转化为二进制,然后一位一位的进行位运算。比如说1Xor4=(001)2 Xor(100)2=(101)2=5。位运算除了具有交换律、结合律这样的普通性质之外,还有几条神奇的性质。
Xor运算的神奇性质之一,就是他自己是自己的逆运算,即对于任何两个布尔变量或者数有(a Xor b)Xor b=a。这一点可以从真值表直接验证。有了这样一个性质,我们就可以把交换两个数的函数swap改进一下。大家应该都知道swap可以这么做:
void swap(int a, int b)
{a=a+b; b=a-b; a=a-b;}
现在我们知道了Xor运算是本身的逆运算之后,就可以把上面的函数改成这个样子:(在C/C++里面把Xor表示为^)
void swap(int a, int b)
{a=a^b; b=a^b; a=a^b;}
乍一看肯定会觉得这个交换函数写的非常诡异,但是仔细一看就知道其原理和刚才那个是一模一样的。而且因为计算机在执行位运算的时候肯定比加减法要快,所以用Xor写的交换函数实际上还更快呢。
这里有一个有意思的小问题:现在给你2n+1个正整数,其中有n对数和1个单独的数,(这里规定一对数的意思是这两个数相等),然后让你设计一种算法,把这个单独的数给找出来,要求时间复杂度为O(n)。比如说这2n+1个数是1 2 …
有趣的无规行走模型
昨天和一帮子同学出去玩,晚饭时间点完菜等待上菜的时候有两个同学玩起了一个非常无聊的游戏:甲同学扔硬币,乙同学猜正反面,如果乙猜对了则乙的鼻子变长1cm,反之如果乙猜错了则鼻子缩短1cm。(这个是和谐过的版本,原始版本变长变短的不是鼻子而是另一个猥琐的东西…)。他们正在无聊的玩,全然不知道这么玩下去他鼻子长度的绝对值期望是多少…其实,这正是我高一的时候在费恩曼物理学讲义上看到的一个数学模型:Random Walk(无规行走)。对于这个模型,我敢说绝大多数人凭直觉会觉得鼻子长度的绝对值最终的期望值会是0,但事实绝非如此,你可以自己扔几次硬币试试,正确的答案应该是你扔硬币次数N的平方根!
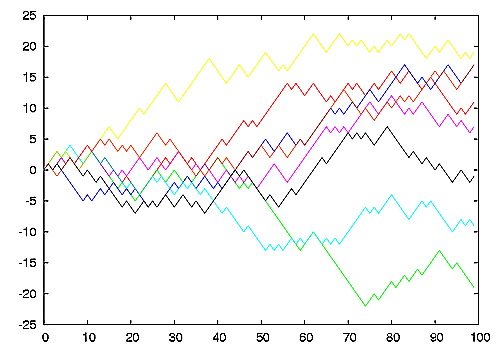
下面给出证明,该证明基本来自《费恩曼物理学讲义》第一卷:…
点猜想
首先在平面上任意给定不全共线N个点,然后在点之间连线,以保证任意两个点之间都有直线连接。所谓点猜想就是说,在这样的情况下,总存在直线仅过两个点。
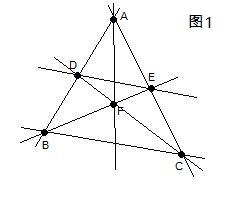 如果给定了A~F六个点的位置如图,则整个图形形状就是左图,DE和AF就仅过两个点。你可以简单尝试一下,试着自己画几个点,你会发现确实无论如何也不能让所有的直线都通过三个或三个以上的点。
如果给定了A~F六个点的位置如图,则整个图形形状就是左图,DE和AF就仅过两个点。你可以简单尝试一下,试着自己画几个点,你会发现确实无论如何也不能让所有的直线都通过三个或三个以上的点。
这个问题是小时候就见过的,在苦苦思索了好一阵子无果之后就给渐渐淡忘了。今天去图书馆看书偶然间又看到这个问题了,觉得还是挺有意思的,不过还是没什么思路。上面的介绍居然说,点猜想在被提出之后几十年内没有人能够证明!看似如此简单的问题居然还难倒了一大批人呢!但是,当最终证明被发现时,虽然思路非常灵活巧妙,却是异乎寻常的简单,连初中生都能看懂!不知你能不能自己证出这个猜想呢?…
棋盘覆盖问题
有一个经典问题:8*8的棋盘,去掉了左下角和右上角2个格子,请问能否用31块1*2的骨牌覆盖整个棋盘。这个问题的答案应该人人都知道吧,染色之后一目了然。
那么,有人要问了:如果去掉的是1红1白的格子各一个,结果是怎样的呢?比如下面的这个图:
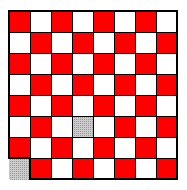
你可以自己画几个图试一试。你能证明一定可以覆盖?还是可以给出反例呢?…
几道有意思的小数学题
1.“一切无理数的无理数次方一定是无理数”,试证明此命题或举出反例。
2.两人在1,2,3,……,9这九个数字中轮流取数,不准重复,谁先取到三数之和为15谁就赢了。问先走者有没有一个稳操胜券的策略?
3.汽油危机已经来临,大家都在叫油荒。分散在长长的环形公路各处的加油站所存的油量仅仅够你跑一圈而无点滴富余。请证明,如果你在一个合适的加油站开始启程,把空油箱加足了汽油,你有充分把握可以跑完一圈,不会中途抛锚。
请先仔细思考再看解答.
…
最小作用量原理与物理之美3——牛顿力学
就像最小作用量原理可以推导出所有几何光学定律一样,力学中也存在一个最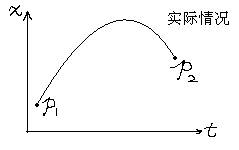 小作用量原理的特例可以推导出整个牛顿力学。今天我们就来研究研究这个。
小作用量原理的特例可以推导出整个牛顿力学。今天我们就来研究研究这个。
有这样一个事实:假定有一个质点在引力场中通过自由运动从某处移动至另一处——你把它抛出去,他就会上升又落下。如果画出x-t图(为了简化,只考虑一维的运动,设x轴是竖直的轴),那么运动图像是一条抛物线。你可以尝试着通过起点和终点画一些别的曲线,如果计算出经历整条路径期间动能减重力势能对时间的积分,你会发现所获得的数值比实际运动所获得的要大。如果我们设作用量S为
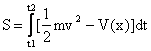
那么上面的事实换句话说就是作用量 S在实际运动中取得最小值。对上面字母的解释:t1、t2表示运动的起点和终点时刻,1/2*m*v^2是研究物体的动能,V(x)是其势能(这里把它写成是随x变化的函数)。当物体只受重力的时候,V(x)=mgx。我们在上一篇文章中说过,一个泛函取得极值可以令其变分等于0,所以在力学中,最小作用量原理的特例就写作:…
S在实际运动中取得最小值。对上面字母的解释:t1、t2表示运动的起点和终点时刻,1/2*m*v^2是研究物体的动能,V(x)是其势能(这里把它写成是随x变化的函数)。当物体只受重力的时候,V(x)=mgx。我们在上一篇文章中说过,一个泛函取得极值可以令其变分等于0,所以在力学中,最小作用量原理的特例就写作:…


