一个电磁学“佯谬”
高中时候看到《费恩曼物理学讲义》第二卷17-4《一个佯谬》的时候,非常困惑,如今终于明白了一些,虽然具体的计算工作还做不了。这个佯谬是这样的: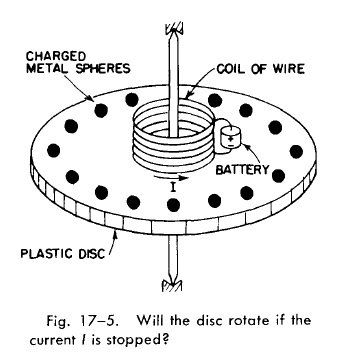
试想构造一个如右图所示的装置。一个绝缘的圆盘通过摩擦力可以完全忽略的轴承套在一个轴上,可以自由旋转。圆盘上,放着一个与之同轴的线圈,通过这个线圈的电流由同样是放在圆盘上的一个小电池提供。圆盘的边缘上固定着一些金属球,注意它们是和圆盘固连在一起的,这些小球每一个都带有一定的电量Q。现在初始条件为有电流通过,整个装置静止不动。
现设想,如果突然切断电源旁的一根导线导致电流变为0,整个圆盘会发生转动吗?电流减小,导致通过线圈的磁通量减少,而磁通量的变化会在空间中激发出感生电场,感生电场的方向为圆形,可以使全部带电的金属球受到圆盘边缘切向方向的力,从而产生一个净力矩导致整个圆盘转起来。然而,从另一个角度来分析,将得出截然相反的结论:因为切断电源的力大小可以忽略,对整个系统没有力矩的贡献,所以整个系统角动量守恒,圆盘仍然将保持不动(整个系统包括圆盘、金属球、线圈以及电源)!
为什么两种途径的分析会产生截然不同的结果呢?真实的物理情景到底是转还是不转呢?…
Project Tuva:费恩曼的演讲视频!
今天在电脑前颓废了一天,当我又在校内网上面闲逛的时候,突然发现留言板上面WLX向我推荐了一个东西,叫做Project Tuva。看到Tuva我立即就想到了Feynman(费恩曼),Tuva(图瓦共和国)是Feynman一生都很想去而最终也没有去成的一个小国家。Google了一下之后找到了Project Tuva的官方网站:http://research.microsoft.com/tuva 。进去一看我便惊喜的快说不出话了:里面是Feynman的7个当年在Cornell大学的演讲视频!我曾经费了好大的事都找不到Feynman当年的演讲视频,如今微软居然收集整理了这些视频并且在网上免费向公众开放!据那上面说是因为Bill Gates本人听过Feynman的演讲并且深受打动受益匪浅,所以微软进行了如此的善举,花重金买下了这7个视频的版权免费提供给公众。这些视频的内容,据细心的LY神牛发现,正是”The Character of Physical Law”(《物理定律的本性》)的内容。想当年高一的时候,我正是在书城闲逛的时候偶然看到了这本书,才从此一发不可收拾的爱上了Feynman,爱上了物理。
http://research.microsoft.com/tuva 热爱物理的人,喜欢Feynman的人,可千万不要错过了这个网站啊!我正在想,是不是每一个热爱物理的人都喜欢Feynman呢?
 …
…
一个很难看出破绽的永动机设计
在《费恩曼物理学讲义 第一卷》第46章中有一个尝试违反热力学第二定律的永动机设计,乍一看貌似还真能实现,我当年就怎么也看不出来这个装置哪里出了问题,最近终于是明白一些了,就写在这里给大家看看吧。
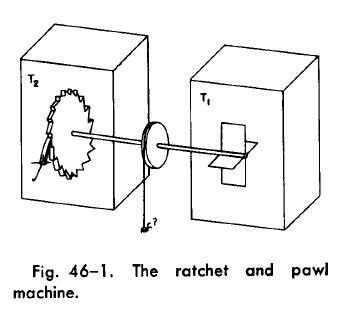
直接用热力学第二定律就可以否定这个装置成功的可能性,但是如果不从力学以及热力学的其他基本定律对该装置予以反驳的话,我始终觉得难以令人信服。那么,到底这套装置哪里出了问题呢?为什么这样的装置不能达到他永动机的目的?
在看我的分析之前,你最好自己仔细思考思考。…
最小作用量原理与物理之美4——构建整个世界
有人曾经问过我有没有一个公式可以描述整个世界,我的回答就是,可能会有,这个定律很可能就是最小作用量原理。《可怕的对称》生动地说道:整个宇宙的终极设计可以写到一张餐巾纸上,那一行紧凑的公式可以推导出所有物理定律。而那张餐巾纸上写的,其实就是作用量S的表达式。我们前面看到了S在几何光学中的特例,也看到了他在经典力学中的特例。终极设计的S中一些量为常数,就可以退化成各种各样的特例。在电磁学、热学、相对论、量子力学中,S也有各自的退化形式。而一旦终极设计的S中的所有项我们都弄清楚了,我们也就可以自豪地宣称我们理解宇宙了。可惜我们离这个梦想还差得很多。
当年20世纪初的时候,物理学大厦貌似被全部推翻了,似乎一切旧的理论都被新的理论所取代了。但是,“在如此多的废墟中间,还有什么东西屹立长存呢?最小作用量原理迄今未经触动,人们似乎相信他会比其他原理更久长。事实上,它是更加模糊,更加抽象。”庞加莱(Poincaré)(又被翻译成彭加勒)如是说。他还说道:“作为普遍的原理,最小作用量原理和守恒原理具有极高的价值,他们是在许多物理定律的陈述中寻求共同点时得到的,因此,他们仿佛代表着无数观察的精髓。”确实,很难想象最小作用量原理会被推翻,因为在最小作用量原理之外我们想不到还有什么更普遍而真实的原理了。现代物理已经全部构建在最小作用量原理之上,如果发现最小作用量原理不成立了,那可以说整个物理就没有什么对的东西了。…
最小作用量原理与物理之美3——牛顿力学
就像最小作用量原理可以推导出所有几何光学定律一样,力学中也存在一个最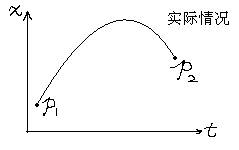 小作用量原理的特例可以推导出整个牛顿力学。今天我们就来研究研究这个。
小作用量原理的特例可以推导出整个牛顿力学。今天我们就来研究研究这个。
有这样一个事实:假定有一个质点在引力场中通过自由运动从某处移动至另一处——你把它抛出去,他就会上升又落下。如果画出x-t图(为了简化,只考虑一维的运动,设x轴是竖直的轴),那么运动图像是一条抛物线。你可以尝试着通过起点和终点画一些别的曲线,如果计算出经历整条路径期间动能减重力势能对时间的积分,你会发现所获得的数值比实际运动所获得的要大。如果我们设作用量S为
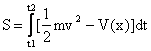
那么上面的事实换句话说就是作用量 S在实际运动中取得最小值。对上面字母的解释:t1、t2表示运动的起点和终点时刻,1/2*m*v^2是研究物体的动能,V(x)是其势能(这里把它写成是随x变化的函数)。当物体只受重力的时候,V(x)=mgx。我们在上一篇文章中说过,一个泛函取得极值可以令其变分等于0,所以在力学中,最小作用量原理的特例就写作:…
S在实际运动中取得最小值。对上面字母的解释:t1、t2表示运动的起点和终点时刻,1/2*m*v^2是研究物体的动能,V(x)是其势能(这里把它写成是随x变化的函数)。当物体只受重力的时候,V(x)=mgx。我们在上一篇文章中说过,一个泛函取得极值可以令其变分等于0,所以在力学中,最小作用量原理的特例就写作:…
最小作用量原理与物理之美2——费马原理
对于几何光学中的许许多多的定律,费马找到了一种统一的描述,现在被称为费马原理,被认为是最小作用量原理在几何光学中的特例,是最小作用量原理最早的成功例子。上一篇文章并没有真正写最小作用量原理,写的仅仅是一些简单的极值问题(千万不要认为那就是最小作用量原理),而本文与下一篇文章则将写最小作用量原理在几何光学与动力学的特例,并给出比较精确的数学公式(这是为了后面的横向比较和更深刻地理解最小作用量原理),对微积分头痛的人可以跳过公式只看文字。
费马原理是这么说的:过空间中两定点的光,实际路径总是光程最短、最长或恒定值的路径。
其中光程定义为该介质的折射率乘以路程。写成数学的形式就是:
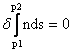
其中,δ是变分符号,p1、p2表示空间中两个固定点,n为介质的折射率,s表示路程。为了理解上式的含义,我们需要和导数做一个类比。我们对一个函数求导数,如果导数值等于零,那么可以判断出原函数在该点处会取得极小值、极大值或恒定值。上面的式子和导数有一个显著的不同,导数研究的是以字母为自变量的函数的极值,而上式想求的则是以一个函数(位置随时间变化的函数)为自变量的泛函的极值。我们把每一条路径看作是位置随时间变化的函数,把这个函数看作自变量,我们要求的则是各条路径中光程取极值的那条路径;就像我们求导求的是各个x中使得y取极值的那个点。函数求极值可以用导数,泛函求极值则可以用变分法,即δS=0(其中S是一个泛函)。大家就把δ理解成和导数相类似的东西就可以了。…


