一张图证明著名等式
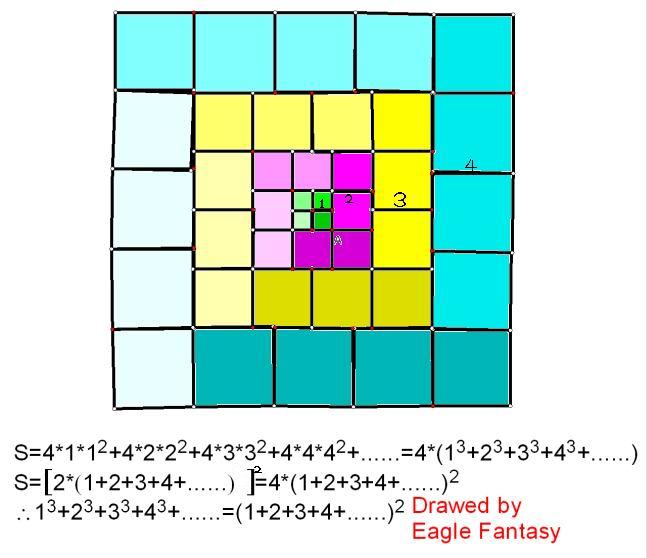
如图,从内到外各圈正方形的边长依次是1,2,3,4……通过面积的两种表达形式,就可以证明结论中的著名等式!
解释一下:第一个算式是把面积一圈一圈加起来,第二个是总边长的平方。…
一个小发现
那天和同学一起讨论时,发现了一个很有意思的东西:
圆的周长公式:C=2*π*R
圆的面积公式:S=π*R^2
这两个公式间,有一个巧妙的联系:对面积公式进行求导即得到周长公式,即dS/dR=C.
球的表面积公式:S=4*π*R^2
球的体积公式:V=4/3*π*R^3
这两个公式间,同样也存在着类似的关系:对体积公式求导即得到表面积公式,即dV/dR=S!!!
我觉得挺有意思的,就上网查了一下有关4维的情形:
“超球”(4维球)的“表体积”公式:V=2*π^2*R^3
“超球”的“超体积”公式:W=1/2*π^2*R^4
(这组公式从网上查的,可能并不很权威,欢迎指出错误之处)
/*update:当时不太明白,现在学了积分了,就一目了然了。就是一圈一圈积分。*/…
有趣的测试你反应能力的一套题
你想测试一下你的反应速度是灵敏还是迟钝么?你想看一看你的聪明程度是否很高么?那么,就请做一下下面这一套提吧,题目很简单,记住,一定要按照顺序作,否则就别做。最后一道题是最考验人的一道题,呵呵,要大约估计一下做这道题的时间。请再作出一道题之前不要看答案,否则没有效果。
1.把这个图形分成全等的两份。…
哥德尔定理
哥德尔定理是数理逻辑中的一个定理,1931年奥地利逻辑、数学家克尔特.哥德尔(Kurt Godel)发现并证明的,这个定理彻底粉碎了希尔伯特的形式主义理想。为理解这个定理及其意义,需要相当的数理逻辑和集合论知识。要把这些预备知识都在这里整理出来,工作太繁重了,这也就是我一直没敢动手写这篇东西的原因之一。这里仍然也不打算详细介绍这些东西,只是在必要的时候给些简单的说明,要想更深刻地理解,有兴趣的朋友可以自学相关课程。
哥德尔定理其实是两个定理,其中哥德尔第一不完备性定理是最重要、也是误解最多的,从这一定理的版本众多就可以看出。如:
“如果一个形式理论T足以容纳数论并且无矛盾,则T必定是不完备的。”
“任何一个相容的数学形式化理论中,只要它强到足以在其中定义自然数的概念,就可以在其中构造在体系中既不能证明也不能否证的命题。”
“任何一个足够强的一致公设系统,必定是不完备的”
第二不完备性定理是第一定理的一个推论:“任何相容的形式体系不能用于证明它本身的相容性”
如果没有相关的知识基础,要理解这个定理真的是比较难。至于证明就更不容易看懂了。我偷点懒,跳过这些直接介绍其意义吧。…

 …
…
