庞加莱的几何学
作者: physixfan最近在看庞加莱(Poincaré)(又被翻译成彭加勒)的《科学与假设》,这是一本闪耀着思想光辉的圣书。介绍科学知识的书很多很多,但是像《科学与假设》这种写科学哲学的书恐怕很难找得到。虽然这本书的语言非常艰涩难懂,但这本书我至少读过3遍,每一遍都能读出一些新的感悟。
在这本书里,庞加莱对几何学提出了几条思想很深刻的见解:
1.几何学公理既非综合判断,也非实验经验,他们是约定。约定是心智的产物,约定的选择是自由的,但又不是随意的。
2.假使自然界没有固体,便不会有几何学。欧几里德几何学的性质与天然固体非常符合。
3.欧几里德几何学不比非欧几何学更真,他只是更为方便而已。经验在任何时候都不会与欧几里德共设相矛盾,同样任何经验永远也不会和罗巴切夫斯基共设相矛盾。
4.可以建立一本词典,把非欧几何的术语和欧几里德几何的术语之间建立一一对应的关系,这样非欧几何将永远不会和欧几里德几何相矛盾。
5.实验告诉我们的是物体之间的相互关系;至于物体与空间的关系,或者空间个部分的互相关系,没有一个实验影响或者能够影响。实验与空间无关,而与物体有关。
为了对非欧几何加以诠释,庞加莱在这本书里提到了著名的庞加莱圆盘模型,这个模型是非常有意思的:
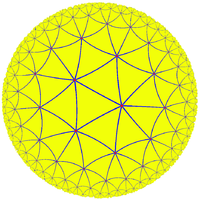 …
…
最近的状态
作者: physixfan去年景年强到我们班介绍经验的时候说保送后的这段时间是很无聊的,还不如在学校里上课幸福,那时我根本不信,可到现在,我是亲身体会了。
自从结果出来之后,我就一直处于比较颓废的浑浑噩噩的状态,整日上网或者看电影,原来的读书计划完全被打乱,背单词的计划也无法完成。现在只是盼着开学,到学校里有了学习的氛围也许会好些。
看有同学在Blog里列了书单,我也把最近打算看的书列出来吧:
《无畏的希望》《什么是数学》《即将来临的经济崩溃》《数学:确定性的丧失》《三重门》《科学与假设》《科学与方法》《科学的价值》《欧亨利小说选》《莫泊桑小说选》《契诃夫小说选》《经济学原理》《梦的解析》《心理学与生活》《矩阵博士的魔法数》《牛奶可乐经济学》《来自圣经的证明》《果壳中的宇宙》《c++primer》《朗道物理学讲义》《费恩曼物理学讲义(第二卷)》………
关于竞赛一等奖取消保送资格
作者: physixfan已经有确切的消息指出,2009年1月1日以后拿到的5科竞赛的省级赛区一等奖不再具有保送资格,只享受高考加20分的优惠。可以说,我是非常非常幸运地赶上了末班车。对于这一突然的政策改变,我有许多话想说。
首先我是非常赞同保送制度的,并不仅仅因为我是既得利益者,而是从国家选拔人才培养人才的方式上来说的。目前的高考制度选拔培养的是全才,虽然我不太认同韩寒所说全面发展等于全面平庸,但是我想给偏才留有一定的机遇总是可以的吧。保送制度正是选拔偏才的一种手段,在任何一个理科学科里做到有所专长便能进入很好的高校继续深造。历史上的大多数伟人不是全才,科学家大多在文史的学习上比较吃力,文史方面有所建树的大师对数理知识一般都知之甚少。我们不能指望培养出来的人才今天证明出来哥德巴赫猜想,明天就写出一部描述心路历程的长篇小说获得普利策文学奖。能够在某一方面有所建树的学生,理应通过一个渠道进入门当户对的大学。当然保送制度也是有缺憾的,一个很明显的缺点就是没有文科的竞赛。以前新概念作文大赛就有保送资格,后来不知道为什么被教育部给取消了。北大招生办的老师说,他们在北大的学生中做了长时间的跟踪调查,保送生的总体成绩要好于高考进来的学生。当保送制度取消了,很多偏才就只能接受二流的教育了。
当然我知道有好多学校有专门的竞赛班,不上其他的课,专门学某一学科,这样做显然是不好的。就像是吃饭时不能喜欢吃肉就只吃肉,多吃一些蔬菜才能使营养更全面。可是如果因为这样的学校存在而废止保送制度,是不是有些因噎废食了。像我们学校,学竞赛只是用课外的时间,停课准备竞赛只是考前几个星期,所有人也都很重视文化课的学习,因为最后能校荐到哪个大学还是根据文化课在学校里的排名决定的,而且据我所知像我们学校这种类型的学校是占了大多数的。现在各大学的保送生考试考的科目还是挺多的,也算是一种导向作用,引导考生们在学竞赛的同时不要偏废,还是要学习各科知识的。要针对竞赛班采取一些措施我是支持的,但是直接取消保送资格这种一刀切的做法我实在不敢苟同。
而且我对教育部这种突然的政策巨变很不满。在我看来,要做出这种重大的政策调整,应该缓慢过度,起码今年下政策说明年入高中那届开始取消保送资格,也比现在这种政策巨变强。对我来说是无所谓了,可是对现在高二的那届学生来说就惨了,学了那么长时间的竞赛一下子失去了意义,对他们是多大的不公平?
有人说太多人为了功利目的而去学竞赛,如今取消了保送资格正好。可是,我们谁人不是为了功利去参加高考?如果不用高考就能上好大学,谁还愿意学那些自己不喜欢的东西?无论高考还是竞赛,都只是一种选拔人才的方式,抱有一定的功利心去参加是再正常不过了。虽然功利心是参加竞赛的动机之一,但是兴趣无疑也是一个重要动机。而且有好多人是在学竞赛的同时对所学的学科越来越有兴趣的。
有人说目前的保送越来越黑,也确实有些人莫名其妙的就得了一等奖,莫名其妙的就保送了。但是不能因为菜刀可以杀人就下令全国不让生产菜刀,教育部完全可以加强对这些后门行为的监督,而不必直接废除保送制度。就像是人的身体长了病就直接判一个人死刑,这不是荒谬的吗。
虽然这些事情已经与我无关了,但是我还是为学弟学妹们鸣不平,对教育部的政策突变感到不满。世界本来是不公平的,但是我希望中国能为人才的选拔提供一个较为公平的环境。以上是我的一些牢骚,就当我没说吧,反正也改变不了事实。…
2009年北京大学保送生、自主招生考试试题及解答
作者: physixfan2009年北京大学保送生、自主招生考试试题及答案(Eagle Fantasy的回忆)
时间:1月1日上午8:30~12:00语文数学英语,下午2:00~4:00物理化学。
语文:(个人觉得比较变态,可能是因为本身语文学得不怎么样)
1.写出两个对成语望文生义的例子
2.改病句
3.对对联:博雅塔前人博雅(注:博雅塔为北大校园内一建筑)
4.古文:一大段古文,没有断句,要求全文翻译(花了我好长时间…)
书杜袭喻繁钦语后[1]·(清)林纾
吴人之归,有绮其衣者[2],衣数十袭[3],届时而易之。而特居于盗乡,盗涎而妇弗觉[4],犹日炫其华绣于丛莽之下[5],盗遂杀而取之。盗不足论,而吾甚怪此妇知绮其衣,而不知所以置其身。夫使托身于荐绅之家[6],健者门焉,严扃深居,盗乌得取?唯其濒盗居而复炫其装[7],此其所以死耳。天下有才之士,不犹吴妇之绮其衣乎?托非其人,则与盗邻,盗贪利而耆杀[8],故炫能于乱邦,匪有全者。杜袭喻繁钦曰:“子若见能不已[9],非吾徒也。”钦卒用其言,以免于刘表之祸[10]。呜呼!袭可谓善藏矣,钦亦可谓善听矣。不尔,吾未见其不为吴妇也。(原文没有标点没有断句)
5.现代文阅读:鲁迅的文章《求乞者》,问了一大堆词的象征意义,问了鲁迅的人生观、行文特点等等
求乞者
我顺着剥落的高墙走路,踏着松的灰土。另外有几个人,各自走路。微风起来,露在墙头的高树的枝条带着还未干枯的叶子在我头上摇动。
微风起来,四面都是灰土。
一个孩子向我求乞,也穿着夹衣,也不见得悲戚,近于儿戏;我烦腻他这追着哀呼。
我走路。另外有几个人各自走路。微风起来,四面都是灰土。
一个孩子向我求乞,也穿着夹衣,也不见得悲戚,但是哑的,摊开手,装着手势。
我就憎恶他这手势。而且,他或者并不哑,这不过是一种求乞的法子。
我不布施,我无布施心,我但居布施者之上,给与烦腻,疑心,憎恶。
我顺着倒败的泥墙走路,断砖叠在墙缺口,墙里面没有什么。微风起来,送秋寒穿透我的夹衣;四面都是灰土。
我想着我将用什么方法求乞:发声,用怎样声调?装哑,用怎样手势?……
另外有几个人各自走路。
我将得不到布施,得不到布施心;我将得到自居于布施之上者的烦腻,疑心,憎恶。
我将用无所为和沉默求乞!……
我至少将得到虚无。
微风起来,四面都是灰土。另外有几个人各自走路。
灰土,灰土,……
……………………
灰土……
6.作文:有一种观点“腐败无害论”,认为腐败是人的本性、可以刺激消费、增进感情、无碍和谐社会,请写一篇文章驳斥这种观点,要求至少正确引用古代诗文5处,800字左右。
数学:(比去年简单了)…
视觉幻象
作者: physixfan下面这段视频是一段有趣的视觉幻象。目不转睛的盯着视频看,记住一定要目不转睛,眼睛不能乱瞟,大约1分钟(30秒其实就够了)之后把目光移向屏幕以外的地方,你是不是发现神奇的事情发生了…世界扭曲了!
…
北京大学2008年保送生和自主招生数学试题答案
作者: physixfan北京大学2008年保送生和自主招生数学试题解答
这套题的难度还是相当大的,这里的解答也不是我一个人做出来的,有我自己做的,有同学帮着做的,也有网上的解答。在网上我还没发现这套题目的完整解答,所以我写了这篇Blog,希望对众多有意考北大的人能够提供一些帮助。
1.证明:边长为1的正五边形的对角线长为(1+√5)/2
证明:经鉴定,这是一道初中数学题,我就不写详细的解答了,用相似三角形就证出来了。
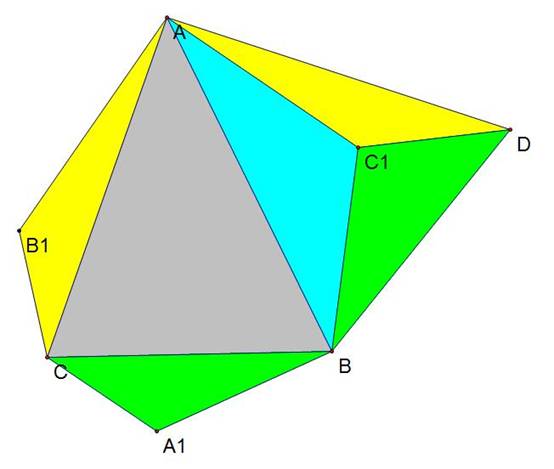
2. 已知一个六边形AB1CA1BC1,AB1=AC1,CB1=CA1,BA1=BC1,∠A+∠B+∠C=∠A1+∠B1+∠C1。证明:三角形ABC面积为六边形的一半。
证明:如图,把三角形AB1C转至AC1D的位置,连接BD,则很明显三角形BDC1与三角形BA1C全等,所以三角形ABC和三角形ADB全等,故三角形ABC面积为六边形的一半。
且min{a1, a2, a3}≤min{b1, b2, b3}
证明:max{a1, a2, a3}≤max{b1, b2, b3}。
证明:令a1 a2 a3为y=x^3+px^2+qx^1+m的三根…


