埃舍尔的数学艺术
作者： physixfan20世纪的伟大艺术家埃舍尔(Escher)是个与众不同的画家，是个和我差不多的数学Geek。他的所有艺术品都不是通常的画作，而是充满数学气息或者是现实中不可能的视觉错觉作品。在所有艺术家中，我最欣赏的就是埃舍尔，甚至甚于达芬奇。虽然埃舍尔的作品初期被当作异类来排斥，但是随着岁月流逝，越来越多的人狂热的喜爱起了他的作品，尤其是对数学有癖好的人。这篇文章将带着大家看看埃舍尔是如何将数学与艺术完美结合。
给大家展示的第一幅画叫《天使与魔鬼》，是我见过的最强的艺术品。这不是一个普通的圆，而是一个非欧几何空间，最早是由庞加莱（Poincaré）（又被翻译成彭加勒）提出了这个模型（参看我的这篇文章）。而填充整个非欧几何空间的，居然是有着强烈反差的白色天使和黑色魔鬼，真是绝了！
…
Phun! 2D physics sandbox
作者： physixfan最近又在You Tube上面看到了介绍Phun的视频，Phun这个小玩意儿对于搞物理的人来说这绝对是个好东西！
什么是Phun呢？Phun是一个2维的物理引擎，在他上面可以画出各种形状的固体，或者倾倒液体，然后加上重力、摩擦力、弹簧、空气阻力、浮力、齿轮等等，他就可以根据真实的物理原理展示出后面将会发生什么。用Phun可以感受到前所未有的真实世界难以实现的物理体验；如果遇到一些物理题想不明白情景，用Phun模拟一下是个不错的选择。
Phun是Umeå大学的学生Emil Ernerfeld为自己的计算机作业而开发的，官方网站http://www.phunland.com，从官网上可以免费下载到他的最新版本，支持Windows\Linux\MacOs。这东西虽好，可是占CPU资源实在太高，我一旦运行Phun.exe，CPU直接占到100%然后卡得要命，没办法只能等弄个好点的电脑在来体验Phun了。
下面是官方演示视频：
…
圆的弦比内接正三角形之边大的概率是多少？
作者： physixfan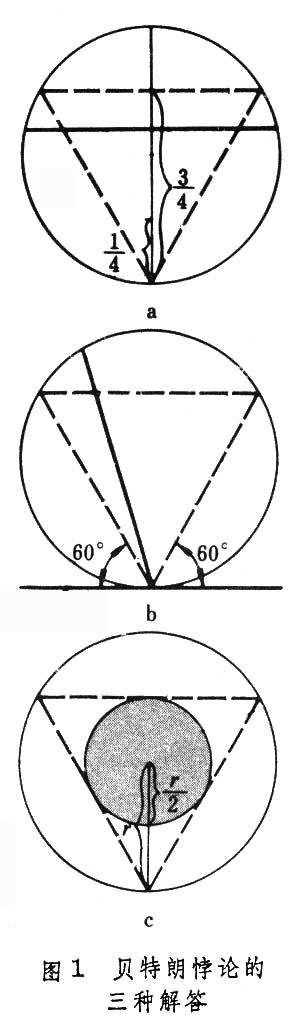
圆的弦比内接正三角形之边大的概率是多少？
偶然间从庞加莱（Poincaré）（又被翻译成彭加勒）的《科学与假设》的概率演算这一章看到了这个命题，他最早由贝特朗提出，故又叫做贝特朗悖论。这一问题有三种解答，答案分别是1/2、1/3和1/4，我怎么也想不清楚到底哪一种是对的，其他的为什么错了，请路过的大牛们帮忙看一看。
解法一：由于对称性，可预先指定弦的方向。作垂直于此方向的直径，只有交直径于1/4 点与 3/4 点间的弦，其长才大于内接正三角形边长。所有交点是等可能的,则所求概率为1/2 。
解法二：由于对称性，可预先固定弦的一端。仅当弦与过此端点的切线的交角在60°～ 120° 之间，其长才合乎要求。所有方向是等可能的，则所求概率为1/3 。
解法三：弦被其中点位置唯一确定。只有当弦的中点落在半径缩小了一半的同心圆内，其长才合乎要求。中点位置都是等可能的,则所求概率为1/4。
这个问题的答案到底应该是多少呢？
顺便说一下，《科学与假设》里有一个观点我很认同，他觉得古典概型中概率的定义不严谨。定义：“若只有有限个不同的基本事件，且每个基本事件发生的可能性是均等的，则事件A的概率等于事件A包含的基本事件数除以基本事件总数。”可是，定义中出现的“可能性是均等的”如何判断？这是不是用概率来定义概率了？这样的定义不算循环定义么？
注：文中的三种解法及图片来自百度百科。…
8月1日去看日食
作者： physixfan我长这么大了还真没见过日食呢，观察日食的机会终于要来了——
今年8月1日，下午19时左右，我国西北地区将迎来一次日全食。青岛虽然没有机会目睹日全食的风貌，但是在日落时分是可以观察到日偏食的。这是21世纪以来，发生在我国境内的首次日全食。
别的地区的情况我就不说了，简单说一下青岛的情况。2008年8月1日18时28分左右的时候，将开始发生日食现象，太阳距离地平线10度左右，太阳直径的90%将被挡住，直到7时左右太阳恢复往日的光亮。我们将可以欣赏残缺的太阳落入地平线的壮丽景象，如果那天不是雾气蒙蒙的话。
估计大家也都很激动，想一睹日食的美景，不过一定要注意千万不可以用肉眼直视太阳，更不要用未经滤光的望远镜观察，否则可能到时永久性失明！！！如果有专业设备，一定要用；如果没有最好去买；如果不想买我们可以用涂黑的玻璃（指的应该是墨镜吧）或者若干张废旧的底片叠在一起或者用废旧软盘的盘芯来有效遮挡阳光。…
Dream Catcher
作者： physixfan剩下的时间不多了
剩下的时间真的不多了
刚刚考完的期末考试考的巨烂无比，都快要突破我能接受的底线了。不过也在意料之中，当数学、物理考完之后我就知道这种简单到我都无语了的题目只能使我考得很差。已经这样了，唯一的办法是忘却这一切。
我们班刚刚班委换届，我很荣幸的被推选为班长。但我有一些迷茫，下个学期一开学那一个月我必定是要去集训的，而那段时间应该正是需要我的时候。我会尽力的。假期老赵让我写工作计划，我可真是头大了啊。
最近几天在家巨颓废，看电影、上网、装系统、睡觉、看闲书是我在家里干的所有事情。不过我已经下定决心以后勤奋学习了，这个假期Blog的更新不会太快，可能还是一周一篇。都已经闲散颓废了整整两年了，在这最关键的2个月，我必须拿出自己全部的心思去学习物理竞赛了。我是一个Dream Catcher，脑子里充满fantasy的Dream Catcher。为了我的梦想，是时候拼搏了！此时不拼更待何时？
最后，再一次用那句我很喜欢的话作为文章结尾：When the dawn comes, tonight will be a memory, too……
狭义相对论重要公式备忘
作者： physixfan写这篇文章的主要目的是为了熟悉一下$$mime\TeX$$的语法…
狭义相对论重要公式
这篇文章中默认不加撇的物理量为S参考系中的量，加撇的物理量为S’参考系中的物理量，其中S’系相对于S系以速度u向x轴方向做匀速运动。注意t表示时刻，而Δt才是表示时间间隔的。
1.时间膨胀效应
假设钟相对于S’系静止，即两次读取时刻在S’系中发生于同一地点，则有$$\Delta t=\frac{\Delta t’}{\sqrt{1-\frac{u^2}{c^2}}}$$
2.动尺缩短效应
假设被测量的物体相对于S’系静止，则$$l=l’\sqrt{1-\frac{u^2}{c^2}}$$…
