physixfan

最小作用量原理与物理之美4——构建整个世界

有人曾经问过我有没有一个公式可以描述整个世界，我的回答就是，可能会有，这个定律很可能就是最小作用量原理。《可怕的对称》生动地说道：整个宇宙的终极设计可以写到一张餐巾纸上，那一行紧凑的公式可以推导出所有物理定律。而那张餐巾纸上写的，其实就是作用量S的表达式。我们前面看到了S在几何光学中的特例，也看到了他在经典力学中的特例。终极设计的S中一些量为常数，就可以退化成各种各样的特例。在电磁学、热学、相对论、量子力学中，S也有各自的退化形式。而一旦终极设计的S中的所有项我们都弄清楚了，我们也就可以自豪地宣称我们理解宇宙了。可惜我们离这个梦想还差得很多。

当年20世纪初的时候，物理学大厦貌似被全部推翻了，似乎一切旧的理论都被新的理论所取代了。但是，“在如此多的废墟中间，还有什么东西屹立长存呢？最小作用量原理迄今未经触动，人们似乎相信他会比其他原理更久长。事实上，它是更加模糊，更加抽象。”庞加莱（Poincaré）（又被翻译成彭加勒）如是说。他还说道：“作为普遍的原理，最小作用量原理和守恒原理具有极高的价值，他们是在许多物理定律的陈述中寻求共同点时得到的，因此，他们仿佛代表着无数观察的精髓。”确实，很难想象最小作用量原理会被推翻，因为在最小作用量原理之外我们想不到还有什么更普遍而真实的原理了。现代物理已经全部构建在最小作用量原理之上，如果发现最小作用量原理不成立了，那可以说整个物理就没有什么对的东西了。…

最小作用量原理与物理之美3——牛顿力学

就像最小作用量原理可以推导出所有几何光学定律一样，力学中也存在一个最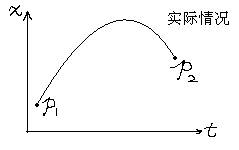小作用量原理的特例可以推导出整个牛顿力学。今天我们就来研究研究这个。

有这样一个事实：假定有一个质点在引力场中通过自由运动从某处移动至另一处——你把它抛出去，他就会上升又落下。如果画出x-t图（为了简化，只考虑一维的运动，设x轴是竖直的轴），那么运动图像是一条抛物线。你可以尝试着通过起点和终点画一些别的曲线，如果计算出经历整条路径期间动能减重力势能对时间的积分，你会发现所获得的数值比实际运动所获得的要大。如果我们设作用量S为

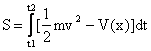
那么上面的事实换句话说就是作用量S在实际运动中取得最小值。对上面字母的解释：t1、t2表示运动的起点和终点时刻，1/2*m*v^2是研究物体的动能，V(x)是其势能（这里把它写成是随x变化的函数）。当物体只受重力的时候，V(x)=mgx。我们在上一篇文章中说过，一个泛函取得极值可以令其变分等于0，所以在力学中，最小作用量原理的特例就写作：…

最小作用量原理与物理之美2——费马原理

对于几何光学中的许许多多的定律，费马找到了一种统一的描述，现在被称为费马原理，被认为是最小作用量原理在几何光学中的特例，是最小作用量原理最早的成功例子。上一篇文章并没有真正写最小作用量原理，写的仅仅是一些简单的极值问题（千万不要认为那就是最小作用量原理），而本文与下一篇文章则将写最小作用量原理在几何光学与动力学的特例，并给出比较精确的数学公式（这是为了后面的横向比较和更深刻地理解最小作用量原理），对微积分头痛的人可以跳过公式只看文字。

费马原理是这么说的：过空间中两定点的光，实际路径总是光程最短、最长或恒定值的路径。
其中光程定义为该介质的折射率乘以路程。写成数学的形式就是：

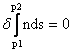
其中，δ是变分符号，p1、p2表示空间中两个固定点，n为介质的折射率，s表示路程。为了理解上式的含义，我们需要和导数做一个类比。我们对一个函数求导数，如果导数值等于零，那么可以判断出原函数在该点处会取得极小值、极大值或恒定值。上面的式子和导数有一个显著的不同，导数研究的是以字母为自变量的函数的极值，而上式想求的则是以一个函数（位置随时间变化的函数）为自变量的泛函的极值。我们把每一条路径看作是位置随时间变化的函数，把这个函数看作自变量，我们要求的则是各条路径中光程取极值的那条路径；就像我们求导求的是各个x中使得y取极值的那个点。函数求极值可以用导数，泛函求极值则可以用变分法，即δS=0（其中S是一个泛函）。大家就把δ理解成和导数相类似的东西就可以了。…

最小作用量原理与物理之美1——自然中无处不在的极值

观察自然界的各种现象，会发现极值往往出现。知道这一点非常重要，在最小作用量被明确提出之前，人们已经研究了很多极值问题。我们先来看一些比较简单的极值问题，会对最小作用量原理有一个更深刻的认识，也能从中看出最小作用量原理的起源与历史。

物理定律都有两种表述形式：一种是普通的我们高中学的形式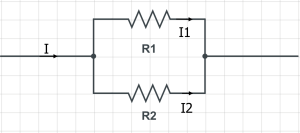，用力、加速度、电场强度等概念描述的物理定律；另一种是极值的形式，在一个物理过程中某个量取得极值。这两种表述形式是等价的。

先看一个最简单的例子，如图，两个电阻R1、R2并联，输入的电流为I，求I1、I2是多少。
这个问题初中生都会做，用并联时电压相等加上欧姆定律就可以作了。可以容易的求得

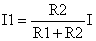
现在我们换一种方法：I1、I2的取值使得热功率最小。…

最小作用量原理与物理之美0——导言

爱因斯坦说过：“我想知道上帝是如何设计这个世界的。对这个或那个现象、这个或那个元素的谱我不感兴趣。我想知道的是他的思想，其他的都只是细节问题。”近代物理隐隐约约的表明，我们人类似乎已经接近于上帝的终极设计了，最小作用量原理、对称与守恒可能就是上帝设计世界的原则。最小作用量原理、对称与守恒不同于F=ma、F=GMm/r^2、F=kx、F=kQq/r^2这类的普通物理定律，他是物理定律的定律，是一切其他普通物理定律的基础。

最小作用量原理是一个令人神往的课题，费恩曼上高中时听到他的老师巴德给他讲的时候就被深深震撼了，我也是一样。当我第一次从费恩曼的书中看到这个原理时，真是有种无法言表的喜悦，好像是我窥见了上帝设计世界的图纸一般。后来我就如饥似渴的学习者有关引人入胜的最小作用量原理的知识，同时越来越被这伟大的原理所吸引。…

希望大家参加LHC@HOME

LHC(the Large Hadron Collider)中文名称为大型强子对撞机，位于日内瓦附近的欧洲粒子物理研究所(CERN)，是所有粒子物理学家翘首以盼的一个项目。原本计划于2007年完工，但由于一些设计失误出现的问题不得不延期，现在还没有竣工。但是它仍然是物理学2008年最值得期待的项目之一，因为LHC的能量足以让我们亲手捕捉到几十年来一直想抓到的“上帝的粒子”——希格斯子，以解释质量的来源，验证标准粒子模型的最重要的预言。同时，LHC也是比较新型的一种加速器，据我了解，以前的加速器加速的往往是电子、反电子，而LHC，像它的名字中表明的一样，加速的是强子（质子就属于强子），新的技术将会带来许多新的发现。不仅仅是验证希格斯子的存在，许许多多的理论将在这里得到验证，许许多多的新发现将在这里诞生。

LHC@HOME主要由欧洲核子研究中心发起，是在家中帮助LHC进行计算的一个项目。大型强子对撞机的稳定运行需要大量的计算。LHC@home 的 SixTrack 程序能够模拟粒子在大型强子对撞机中运行从而研究其稳定性。它计算校检对撞机中运行的高能粒子束的长期稳定性所必需的数据，使项目负责人能够洞察对撞机将来的运行情况。…