2020年投资回顾
作者: physixfan2020年真的是不平凡的一年。疫情刚开始的时候我还以为今年的投资收益率只要是正的就满足了,万万没想到后面居然是这样的剧情… 年末了,计算了一下我今年所有账户总的收益率 (IRR):36%左右(注:没计算现金 也没计算币市)。和纳指 QQQ (+46%) 相比还是差了一截,不过和标普500指数 VOO (+16%) 相比的话也算是跑赢了吧😂
美股股债平衡
今年我的最大仓位是美股这边的股债平衡策略,股票和债券都买,然后杠杆率我会根据情况而调整。年初时候我觉得美股有点高位,于是主要仓位都是没有杠杆的 VOO+TLT。后来3月大跌时候我真的很开心,终于等到了美股也能变便宜了。3月下跌趋势下我没有加仓加杠杆,但是4月反弹开始了之后我就开始加仓加杠杆了:4月时候兑现了积攒多年的MR点数换出来了3万多USD的现金然后立刻丢进了股市,然后把杠杆率从1.0x提升到了1.5x(主要是买了自带1.5x杠杆的股债平衡基金NTSX)。当时也完全没想到后面居然就是这样一路涨了上来,本来还想着后面如果再跌还得继续加杠杆呢。没想到啊没想到,后面竟是一路的直线上涨,就这样1.5x的杠杆率保持了大半年。然后到了9月我又觉得美股实在是太高了,于是又开始逐渐降低杠杆率。
A股ASHR
在2019年投资回顾中我写到我有挺大的A股仓位,主要就是买的沪深300基金 ASHR。虽然好像大部分人都不看好A股,但今年A股的涨势其实比美股SP500指数更加猛烈,ASHR 今年涨了+33%,是比VOO的+16%高的(当然和纳指相比还是比不过)。今年一整年我都基本没有买入卖出 ASHR,只是持有不动。目前来看A股还不算是大泡沫时期,还是可以继续hold的。
投资中国其实只买沪深300还不够,还需要买海外上市的中概股(可以考虑MCHI或FLCH)才完整,不过2020年政治方面的风险一直挺大,我在担心在美上市中概股的安危,同时在前半年美股的价格比较有吸引力,所以一直没有买入中概股基金。其实还是该买的,明年估计会加仓中概股,以达到目标比例。
小赌怡情个股
今年买的小赌怡情个股简直是大爆发… TSLA 今年一年就涨了5倍,从我买入算起的话总共有10倍多的收益率了。我买着玩的其他个股,像是AAPL,AMZN,TCEHY,JPM,AXP等等这些今年都有巨大的涨幅。这是个奇怪的年份,散户随便买那种热门股票都能赚翻… …
如何计算自己的投资回报率?TWR 时间加权收益率 vs IRR 内部收益率(更新)
作者: physixfan这几天想看看自己这半年来的投资回报率如何,意识到如何计算投资回报率并不是一件完全trivial的事情,各券商直接给出来的数字可能也有不同的定义。其原因在于需要考虑资金流入流出的影响。
Basic Rate of Return
最naive的想法是,计算投资回报率就直接把一段时间内的利润除以本金即可,即:
Basic Return = (EV – BV) / BV
其中EV是Ending Value, BV是Beginning Value。但是有资金的流入流出怎么办?最naive的方法就是把净资金流入算作本金,即:
Basic Return = [EV – (BV+CF)] / (BV+CF)
其中CF是 Net Cash Flow。这样计算,最大的好处自然是简单粗暴;但是有一个致命问题就是,当资金流入流出很多或很大的时候,会让结果变得不准确。
举一个简单而极端的例子:假设年初投入本金$1千,某一天投入资金$1百万,一天后涨了1%赚了$1万之后把这$1百万撤走了,到了年末的时候,投资的股票价格正好跌回和年初一样。这样的话,这一年中净资金流入CF为0,本金BV为$1千,而EV是$1.1万,最后计算回报率的时候如果按上面公式计算分母(BV+CF)是$1千,于是回报率1000%。显然,这个结果没有任何意义。
大家每个月都有新的收入进来,都会投入到股市当中,因此资金的流入流出肯定是投资的重要一部分,因此 Basic Rate of Return 这种计算投资回报率的方式基本上可以说是错误计算方式了。而正确的计算方式有两种:时间加权收益率 Time-Weighted Return (TWR) …
相位同步与藏本模型 (Phase Synchronization and Kuramoto Model) 的形象展示
作者: physixfan在读PhD的时候,有一门课讲到了相位同步 Phase Synchronization 的现象(藏本模型 Kuramoto Model),当时学的似懂非懂。今天偶然看到了一个实验视频(原地址是 https://www.youtube.com/watch?v=Aaxw4zbULMs,在墙外),直观的展示了相位同步现象。鉴于这方面的中文资料非常少,就发布一下这篇文章喂给搜索引擎吧,希望以后大家用中文搜索相关内容的时候也能看得到这个直观的视频。
相位同步现象属于我比较感兴趣的那类现象:设定非常简单,就是简谐振动+弱耦合而已,完全属于经典力学的范畴内一点玄学都没有,但是却可以产生非常 non-trivial、反直觉的结果。还有一个类似的例子是倒立单摆的稳定性与 ponderomotive force。
至于为什么这个简单的实验装置是藏本模型 Kuramoto Model 的一个具体实现,见这篇文章:
至于为什么藏本模型 Kuramoto Model 是一个很普遍的模型,在很多完全不同的物理系统中都可以出现,感兴趣的话可以阅读更多资料,例如:
…手上有一大笔钱 应该一次性投入 (Lump Sum (LS)) 还是定投 (Dollar Cost Averaging (DCA))?
作者: physixfan手上有一大笔钱,应该一次性投入 (Lump Sum (LS)),还是分成若干份然后在一两年的时间里均匀的定投 (Dollar Cost Averaging (DCA)) ?这个问题最近好多朋友都在问我。简单来说,这两个方案的主要区别是:一次性投入的期望收益更高一点,但是可能产生的最大回撤也更大一点。
美股的历史实在是太过辉煌,看大体趋势的话基本就是永远涨的态势,因此用历史数据做回测的话,甚至都不用具体做研究就能猜到,结论肯定是越早投入收益越高。这就类似于手上攒出来了一大笔钱,又需要在北京买房的话,问应该今年买还是两三年后买,那大家肯定都会不假思索的说应该今年买,早买早超生。实际用美股的历史数据做回测的结果也正如直观上想的一样,就是一次性投入期望收益更高。
一次性投入的缺陷就是最大回撤可能比较高。如果你很不幸把辛辛苦苦攒的钱在2000年初的最高点一次性丢进了纳斯达克指数基金QQQ,那你将面临的将是连续3年负百分之三十几的可怕大幅回撤。如果这笔钱是分成一两年时间定投的,那么回撤幅度就会小很多。问标题里的问题的朋友,一般是初入股市的新手,大幅回撤恐怕会造成严重的心理不适感。定投的好处就是股市跌了一些的话手上也还有现金可以加仓,会让人心理上感觉好一点。当然,更大概率会发生的事情依然是股市每年都在继续节节攀升,定投到后面成本越来越高。其实定投更适用的场景是每月工资一到账就立刻丢进股市(401K账户就是在做这件事),而不是手上已经有一大笔钱的情况下该怎么办。
当然,一次性投入和定投也不是完全互斥的,你也完全可以先一次性投入一半资金,剩下的一半再定投一两年。
其实,问我这个问题的朋友们,一般情况都是手上的“一大笔钱”是自己刚开始工作几年攒下的一笔钱,这笔钱的绝对金额,和将来每月攒钱进股市一直到退休相比,并不是一笔特别大的钱。之所以想点明这一点,是想说在纠结这个问题的朋友们其实没有必要太过焦虑或纠结,其实怎么选都可以。你现在读到了这篇文章,说明你对投资有了一定的认识,知道钱不能躺在银行账户里了需要投资了,这就已经很不错了。至于到底这笔钱是一次性投入了还是定投了,最后产生的效果不会差别很大,即使有差别也多半是来自自己不能控制的随机因素而已。当然,如果你手上的这一大笔钱是突然继承了几千万刀这种,就当我这段话没说吧😂
总结一下就是,一次性投入 vs 定投,这个问题没有标准答案,一次性投入期望收益更高但可能产生的最大回撤也更大,我个人认为怎么选都可以,只要你心理舒适就好。…
Risk Parity 的具体含义,以及与 Inverse Volatility 的区别与联系
作者: physixfan在《Adaptive Risk Parity 投资策略:动态调整UPRO和TMF的比例》及相关文章的评论区里,有不少朋友不满足于UPRO和TMF这两个投资标的,而是还想加入TQQQ或者UGLD等一起按 Risk Parity(风险平价)的思想来投资。我个人不打算投资这些其他的标的,但是其他人这样投资我也不会强烈反对。
但是有一个问题需要注意一下:Risk Parity 并不总是等价于 Inverse Volatility。在那篇文章里提到的网友分享的Github代码,实际上计算的是 Inverse Volatility。只有投资标的数量为2的时候 Risk Parity 才等价于 Inverse Volatility!
Risk Parity 的定义
下面我来讲一下 Risk Parity 的具体含义,以及为什么它在除了N=2的时候并不等价于 Inverse Volatility。
Wikipedia 上对 Risk Parity 的介绍就写的不错:Risk …
股市回报率的时间尺度问题
作者: physixfan我意识到上一篇文章《凯利判据在美股中的应用:计算最佳杠杆率》可能会导致一些本不适合加杠杆的朋友跟风加杠杆,因此我这篇文章想强调这样一个理念:如果你的一笔钱在一两年内就有可能用到,那么这笔钱千万不要加杠杆投资,甚至连进股市都不应该;只有当这笔钱至少在15+年的时间尺度上保证不会需要被迫卖出的情况下,才应当采用最大化log return等目标进而加杠杆。
关于这个理念,Expect the Unexpected 的这篇文章讲的相当到位。引用一下他做的几张精彩的图来讲解一下:
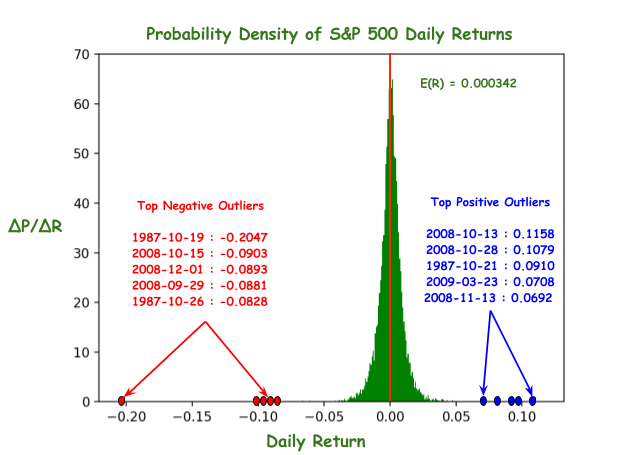
这张图是标普500指数每天的回报率的 PDF (Probability Density Function)。看上去非常随机,没有什么有意义的规律可言。那如果我们看间隔一定天数 (ΔT) 之后的日均回报率,会如何呢?接下来就是见证奇迹的时刻:
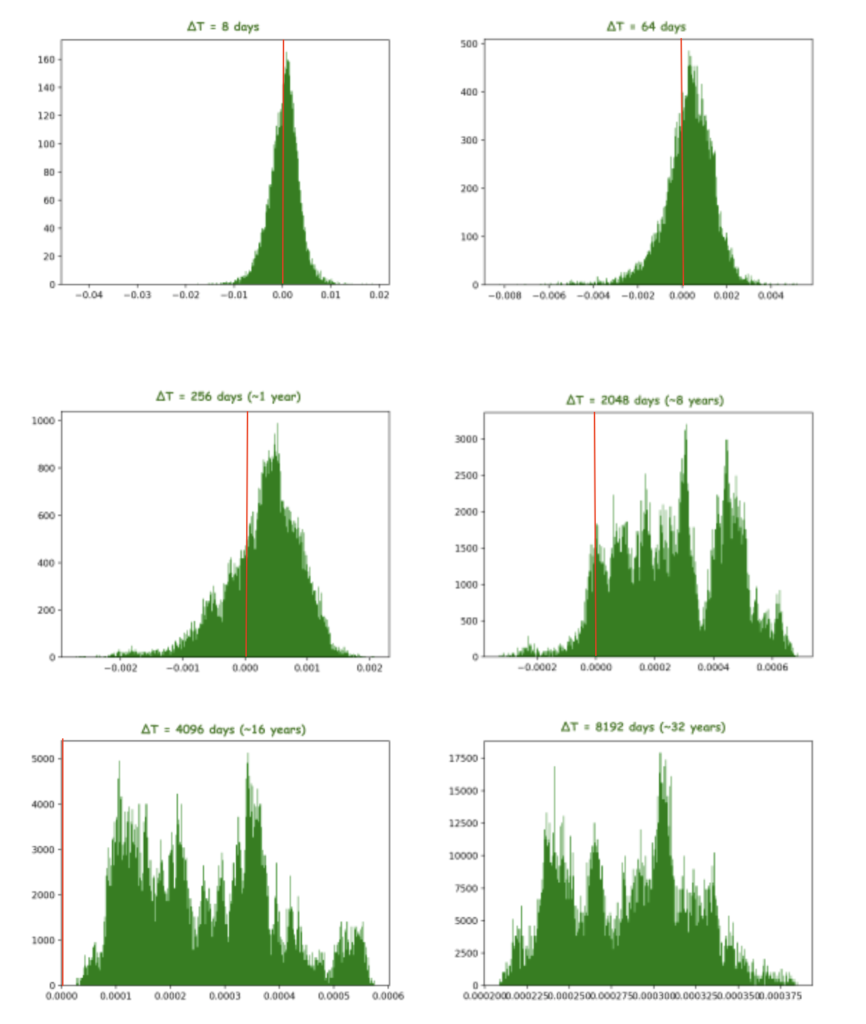
这张图是间隔8天、64天、256天(~1年)、2048天(~8年)、4096天(~16年)、8192天(~32年)的股市日均回报率的PDF。可以看到在间隔天数比较小的时候,分布还只是看起来越来越宽了而已;然而当间隔在1年左右的时候开始,回报率的峰值就明显偏正了,回报率为正的概率已经明显的大于负了;真正的奇迹在间隔16年和32年的图中,整个分布几乎全部在正的一侧了!
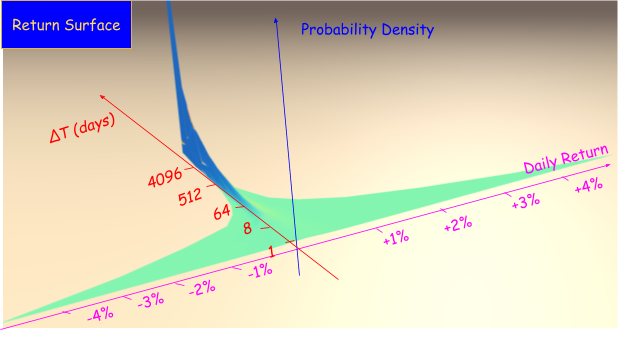
这张图是把各个间隔日数的PDF画在一起的图,是一张非常直观而信息量满满的图。可以说所有自称能预测第二天股市涨跌的人都是神棍;但我可以说我有极大的把握预测30年后的股市点位比今天高!时间尺度越长,这个论断的确定性就越大。
很多年轻人可能觉得自己现在手里的资金量太小,在投资方面比年长的人劣势太大。然而我却认为,年轻在投资方面有一个非常非常大的优势:Time Horizon 足够长。一个30岁的人,他大概率在接下来的30年内都可以做股市的净买入者,一点股票都不卖出。这样一来,在30年的时间尺度上,股市回报的确定性实在是太大了!
借着这篇文章我想在结尾处再强调一下:本站上几乎所有提到杠杆的投资类文章,全部都假设你有至少15+年的投资 time horizon,如果你投资的这笔钱在短时间内就有可能用得到(比如需要买房),那么切不可盲目追求最大化 log return,千万不要加杠杆!…