physixfan

最小作用量原理与物理之美1——自然中无处不在的极值

观察自然界的各种现象，会发现极值往往出现。知道这一点非常重要，在最小作用量被明确提出之前，人们已经研究了很多极值问题。我们先来看一些比较简单的极值问题，会对最小作用量原理有一个更深刻的认识，也能从中看出最小作用量原理的起源与历史。

物理定律都有两种表述形式：一种是普通的我们高中学的形式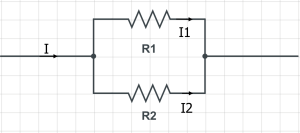，用力、加速度、电场强度等概念描述的物理定律；另一种是极值的形式，在一个物理过程中某个量取得极值。这两种表述形式是等价的。

先看一个最简单的例子，如图，两个电阻R1、R2并联，输入的电流为I，求I1、I2是多少。
这个问题初中生都会做，用并联时电压相等加上欧姆定律就可以作了。可以容易的求得

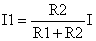
现在我们换一种方法：I1、I2的取值使得热功率最小。…

最小作用量原理与物理之美0——导言

爱因斯坦说过：“我想知道上帝是如何设计这个世界的。对这个或那个现象、这个或那个元素的谱我不感兴趣。我想知道的是他的思想，其他的都只是细节问题。”近代物理隐隐约约的表明，我们人类似乎已经接近于上帝的终极设计了，最小作用量原理、对称与守恒可能就是上帝设计世界的原则。最小作用量原理、对称与守恒不同于F=ma、F=GMm/r^2、F=kx、F=kQq/r^2这类的普通物理定律，他是物理定律的定律，是一切其他普通物理定律的基础。

最小作用量原理是一个令人神往的课题，费恩曼上高中时听到他的老师巴德给他讲的时候就被深深震撼了，我也是一样。当我第一次从费恩曼的书中看到这个原理时，真是有种无法言表的喜悦，好像是我窥见了上帝设计世界的图纸一般。后来我就如饥似渴的学习者有关引人入胜的最小作用量原理的知识，同时越来越被这伟大的原理所吸引。…

希望大家参加LHC@HOME

LHC(the Large Hadron Collider)中文名称为大型强子对撞机，位于日内瓦附近的欧洲粒子物理研究所(CERN)，是所有粒子物理学家翘首以盼的一个项目。原本计划于2007年完工，但由于一些设计失误出现的问题不得不延期，现在还没有竣工。但是它仍然是物理学2008年最值得期待的项目之一，因为LHC的能量足以让我们亲手捕捉到几十年来一直想抓到的“上帝的粒子”——希格斯子，以解释质量的来源，验证标准粒子模型的最重要的预言。同时，LHC也是比较新型的一种加速器，据我了解，以前的加速器加速的往往是电子、反电子，而LHC，像它的名字中表明的一样，加速的是强子（质子就属于强子），新的技术将会带来许多新的发现。不仅仅是验证希格斯子的存在，许许多多的理论将在这里得到验证，许许多多的新发现将在这里诞生。

LHC@HOME主要由欧洲核子研究中心发起，是在家中帮助LHC进行计算的一个项目。大型强子对撞机的稳定运行需要大量的计算。LHC@home 的 SixTrack 程序能够模拟粒子在大型强子对撞机中运行从而研究其稳定性。它计算校检对撞机中运行的高能粒子束的长期稳定性所必需的数据，使项目负责人能够洞察对撞机将来的运行情况。…

宇宙中神秘的大数

物理学中有很多常数，有一些是带有量纲的，比如光速c，万有引力常数G，电子的电荷量e……还有一部分则是无量纲的常数，比如精细结构常数α(α=e²/(2*ε₀*h*c≈1/137。关于其更详细的解释，请看这里)。我们感兴趣的是后者，因为后者的数量是不随单位的任意选取而变化的。比如说我们把米定义为现在的米的1000倍，那么光速c的大小就变了，他在数值上就成了原来的1/1000；但是无量纲的数，比如精细结构常数α，他的数值大小并不会因此而变化。可以说，无量纲的常数实际上是宇宙的某种性质。

关于几个无量纲的常数，存在着某种神秘的关系。
万有引力耦合常数是c₁=G*m_p²/c=5*10^-39
质子和电子间的静电力与万有引力之比是 c₂=(e²)/(G*m_p*m_e)=2*10³⁹
宇宙的年龄除以光穿过一个经典电子需要的时间是 c₃=(m_e*c³)/(e²*H)=7*10³⁹
宇宙的总质量除以质子的质量是 c₄…